HyperLogLog学习

本文参考文章：

论文原文：

HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm

HyperLogLog仿真网站：

Sketch of the Day: HyperLogLog — Cornerstone of a Big Data Infrastructure – AK Tech Blog (neustar.biz)

问题

如果你负责开发维护一个大型的网站，现在需要网站每个网页每天的 UV 数据，然后让你来开发这个统计模块，你会如何实现？

如果统计 PV 只需要每个网页一个独立的 Redis 计数器就行，这个计数器的 key 后缀加上当天的日期。这样来一个请求，incrby 一次，最终就可以统计出所有的 PV 数据。

但是 UV 不一样，它要去重，同一个用户一天之内的多次访问请求只能计数一次。这就要求每一个网页请求都需要带上用户的 ID，无论是登陆用户还是未登陆用户都需要一个唯一 ID 来标识。

你也许已经想到了一个简单的方案，那就是为每一个页面一个独立的 set 集合来存储所有当天访问过此页面的用户 ID。当一个请求过来时，我们使用 sadd 将用户 ID 塞进去就可以了。通过 scard 可以取出这个集合的大小，这个数字就是这个页面的 UV 数据。没错，这是一个非常简单的方案。

但是，如果你的页面访问量非常大，比如一个爆款页面几千万的 UV，你需要一个很大的 set 集合来统计，这就非常浪费空间。如果这样的页面很多，那所需要的存储空间是惊人的。为这样一个去重功能就耗费这样多的存储空间，值得么？其实需要的数据又不需要太精确，105w 和 106w 这两个数字并没有多大区别，So，有没有更好的解决方案呢？

HashMap

Java中的HashSet本质是Value值相同的HashMap，假设HashMap的Key为String，Value为bool，当网页有百万人访问时，此HashMap所占用的内存空间为：100万 *（String + bool），而这还只是一个网页的占用。

占用太大，基本不用考虑。

B树

B树最大的优势是插入和查找效率很高，如果用B树存储要统计的数据，可以快速判断新来的数据是否已经存在，并快速将元素插入B树。要计算基数值，只需要计算B树的节点个数。将B树结构维护到内存中，可以快速统计和计算，但依然存在问题，B树结构只是加快了查找和插入效率，并没有节省存储内存。例如要同时统计几万个链接的UV，每个链接的访问量都很大，如果把这些数据都维护到内存中，实在是够呛。

bitmap

bitmap可以理解为通过一个bit数组来存储特定数据的一种数据结构，每一个bit位都能独立包含信息，bit是数据的最小存储单位，因此能大量节省空间，也可以将整个bit数据一次性load到内存计算。如果定义一个很大的bit数组，基数统计中每一个元素对应到bit数组的其中一位，例如bit数组 001101001代表实际数组[2,3,5,8]。新加入一个元素，只需要将已有的bit数组和新加入的数字做按位或 (or)计算。bitmap中1的数量就是集合的基数值。

bitmap有一个很明显的优势是可以轻松合并多个统计结果，只需要对多个结果求异或就可以。也可以大大减少存储内存，可以做个简单的计算，如果要统计1亿个数据的基数值，大约需要内存：
$$
100000000/8/1024/1024 \approx12M
$$
如果用64(或者32)bit的long(或者int)代表每个统计数据，大约需要内存：
$$
64(或者32)*100000000/8/1024/1024 \approx 762(或者381)M
$$
bitmap对于内存的节约量是显而易见的，但还是不够。统计一个对象的基数值需要12M，如果统计10000个对象，就需要将近120G了，同样不能广泛用于大数据场景。

概率算法

实际上目前还没有发现更好的在大数据场景中准确计算基数的高效算法，因此在不追求绝对准确的情况下，使用概率算法算是一个不错的解决方案。概率算法不直接存储数据集合本身，通过一定的概率统计方法预估基数值，这种方法可以大大节省内存，同时保证误差控制在一定范围内。目前用于基数计数的概率算法包括:

Linear Counting(LC)：早期的基数估计算法，LC在空间复杂度方面并不算优秀，实际上LC的空间复杂度与上文中简单bitmap方法是一样的（但是有个常数项级别的降低），都是
$$
O(N_{max})
$$
LogLog Counting(LLC)：LogLog Counting相比于LC更加节省内存，空间复杂度只有
$$
O(log_2(log_2(N_{max})))
$$
HyperLogLog Counting(HLL)：HyperLogLog Counting是基于LLC的优化和改进，在同样空间复杂度情况下，能够比LLC的基数估计误差更小。

HyperLogLog

上面我们计算过用bitmap存储1亿个统计数据大概需要12M内存；而在HLL中，只需要不到1K内存就能做到；redis中实现的HyperLogLog，只需要12K内存，在标准误差0.81%的前提下，能够统计2^64个数据。那么概率算法是怎样做到如此节省内存的，又是怎样控制误差的呢？

伯努利实验

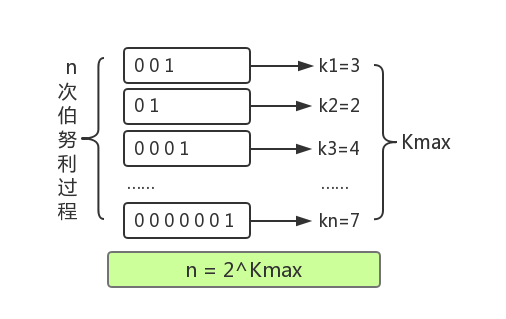
最终结合极大似然估算的方法，发现在n和kmax中存在估算关联：n = 2^(Kmax) 。这种通过局部信息预估整体数据流特性的方法似乎有些超出我们的基本认知，需要用概率和统计的方法才能推导和验证这种关联关系。

n次伯努利实验

分桶平均

HLL的基本思想是利用集合中数字的比特串第一个1出现位置的最大值来预估整体基数，但是这种预估方法存在较大误差，为了改善误差情况，HLL中引入分桶平均的概念。
同样举抛硬币的例子，如果只有一组抛硬币实验，运气较好，第一次实验过程就抛了10次才第一次抛到正面，显然根据公式推导得到的实验次数的估计误差较大；如果100个组同时进行抛硬币实验，同时运气这么好的概率就很低了，每组分别进行多次抛硬币实验，并上报各自实验过程中抛到正面的抛掷次数的最大值，就能根据100组的平均值预估整体的实验次数了。

具体来说，就是将哈希空间平均分成m份，每份称之为一个桶（bucket）。对于每一个元素，其哈希值的前k比特作为桶编号，其中 2k=m ，而后L-k个比特作为真正用于基数估计的比特串。

桶编号相同的元素被分配到同一个桶，在进行基数估计时，首先计算每个桶内元素最大的第一个“1”的位置，设为M[i]，然后对这m个值取平均后再进行估计，

下面举一个例子说明分桶平均怎么做。

假设H的哈希长度为16bit，分桶数m定为32。

设一个元素哈希值的比特串为“0001001010001010”，由于m为32，因此前5个bit为桶编号，所以这个元素应该归入“00010”即2号桶（桶编号从0开始，最大编号为m-1）

而剩下部分是“01010001010”且显然ρ(01010001010)=2，所以桶编号为“00010”的元素最大的ρ即为M[2]的值。

调和平均数

LLC中使用几何平均数预估整体的基数值，但是当统计数据量较小时误差较大；HLL在LLC基础上做了改进，采用调和平均数，调和平均数的优点是可以过滤掉不健康的统计值，具体的计算公式为：
$$
H = \frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+…+\frac{1}{x_n}} = \frac{n}{\sum_{i=1}^{n}\frac{1}{x_i}}
$$

偏差修正

虽然调和平均数能够适当修正算法误差，但作者给出一种分阶段修正算法。当HLL算法开始统计数据时，统计数组中大部分位置都是空数据，并且需要一段时间才能填满数组，这种阶段引入一种小范围修正方法；当HLL算法中统计数组已满的时候，需要统计的数据基数很大，这时候hash空间会出现很多碰撞情况，这种阶段引入一种大范围修正方法。最终算法用伪代码可以表示为如下

m = 2^b   # with b in [4...16]
 
if m == 16:
    alpha = 0.673
elif m == 32:
    alpha = 0.697
elif m == 64:
    alpha = 0.709
else:
    alpha = 0.7213/(1 + 1.079/m)
 
registers = [0]*m   # initialize m registers to 0
 
###########################################################################
# Construct the HLL structure
for h in hashed(data):
    register_index = 1 + get_register_index( h,b ) # binary address of the rightmost b bits
    run_length = run_of_zeros( h,b ) # length of the run of zeroes starting at bit b+1
    registers[ register_index ] = max( registers[ register_index ], run_length )
##########################################################################
# Determine the cardinality
DV_est = alpha * m^2 * 1/sum( 2^ -register )  # the DV estimate
if DV_est < 5/2 * m: # small range correction
    V = count_of_zero_registers( registers ) # the number of registers equal to zero
    if V == 0:  # if none of the registers are empty, use the HLL estimate
          DV = DV_est
    else:
          DV = m * log(m/V)  # i.e. balls and bins correction
if DV_est <= ( 1/30 * 2^32 ):  # intermediate range, no correction
     DV = DV_est
if DV_est > ( 1/30 * 2^32 ):  # large range correction
     DV = -2^32 * log( 1 - DV_est/2^32)